【论文笔记】Graph attention networks
Veličković P, Cucurull G, Casanova A, et al. Graph attention networks[J]. arXiv preprint arXiv:1710.10903, 2017.
我们提出了图注意网络(GATs),这是一种新颖的神经网络架构,可以在图结构数据上运行,利用隐藏的自注意层来解决基于图卷积或其近似的先前方法的缺点。通过堆叠层,其中的节点能够参与其邻居的特征,我们可以(隐式地)为邻居中的不同节点指定不同的权重,而不需要任何昂贵的矩阵操作(例如反转)或依赖于预先知道的图结构。
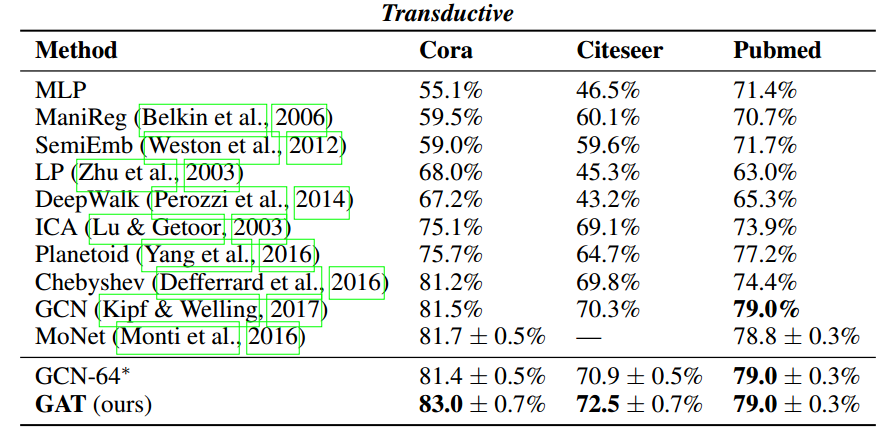
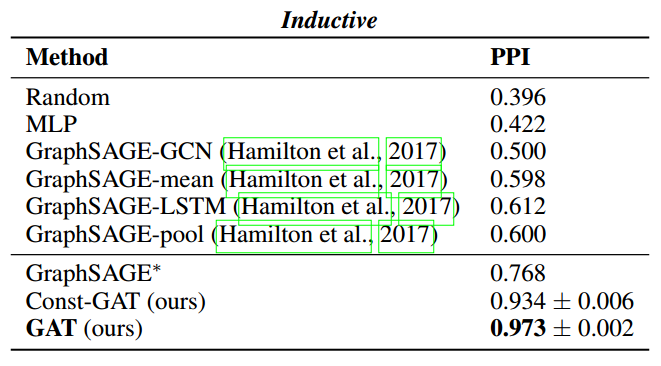
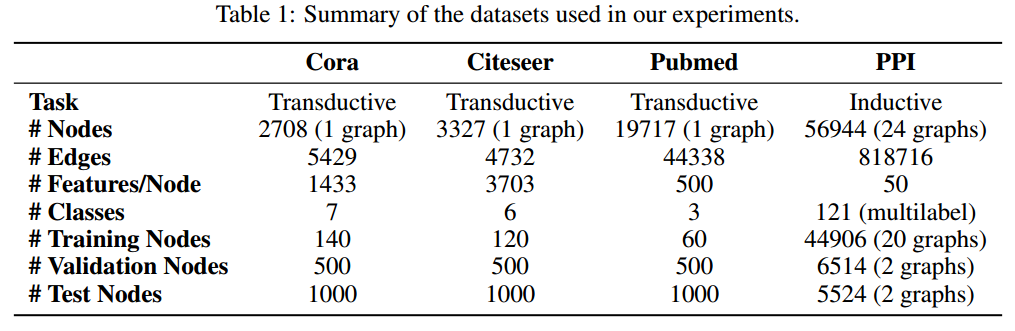
通过这种方式,我们同时解决了基于频谱的图神经网络的几个关键挑战,并使我们的模型很容易适用于感应和转导问题。我们的GAT模型已经在四个已建立的传导和归纳图基准中达到或匹配了最先进的结果:Cora, Citeseer和Pubmed引文网络数据集,以及蛋白质-蛋白质相互作用数据集(其中测试图在训练期间保持不可见)。
GAT结构
GA层的输入是一组节点特征: $$ \bold{h}={\vec{h}_1,\vec{h}_2,…,\vec{h}_N},\vec{h}_i\in \mathbb{R}^F $$ 其中,$N$是节点的数量,$F$是每个节点的特征数量。GA层的输出是一组新的节点特征: $$ \bold{h}’={\vec{h}_1’,\vec{h}_2’,…,\vec{h}_N’},\vec{h}_i’\in \mathbb{R}^{F’} $$ 参数含义同理。
为了学习到更高层的特征,引入可学习的线性变换。每个节点应用共享线性变换: $$ e_{ij}=a(\bold{W}\vec{h_i},\bold{W}\vec{h_j}) $$ 这表示出了节点j对节点i的重要性。最一般情况下,所有节点都可以注意到每一个节点,但是这种做法会丢失图的结构信息,因此选择只关注一阶邻居,称为带掩码的图注意力。
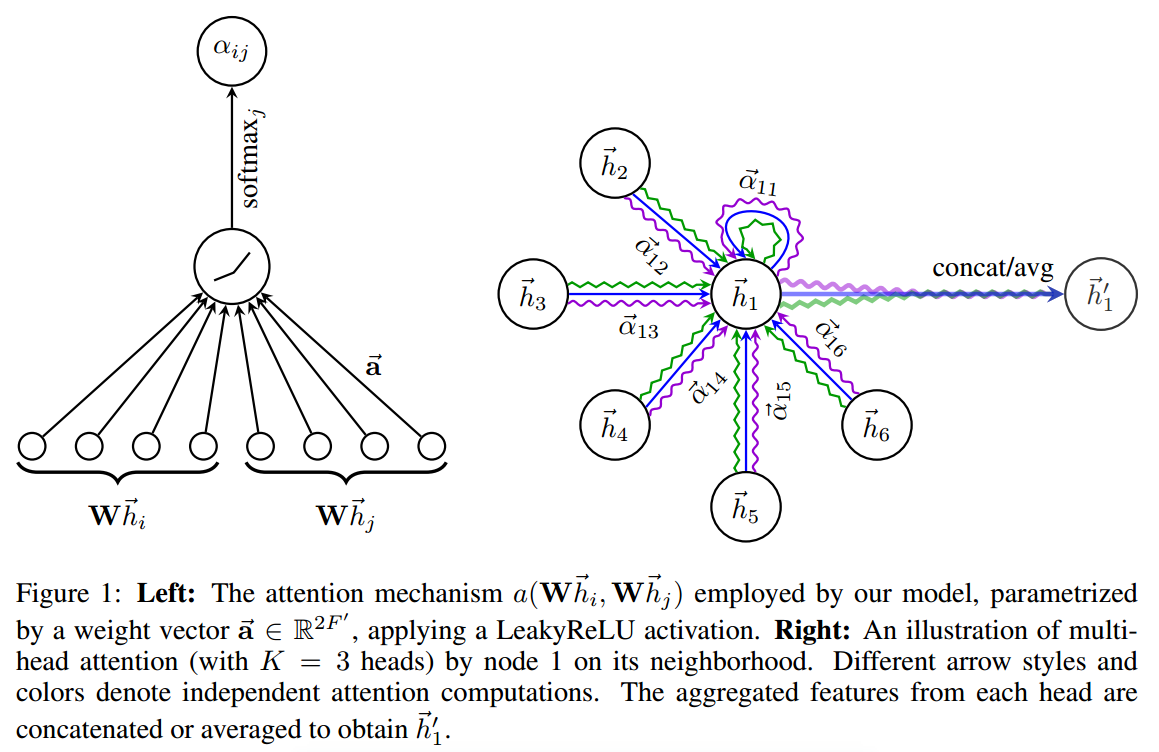
为了使不同节点的系数易于比较,在本文实验中,用softmax将其归一化: $$ \alpha_{ij}=softmax_j(e_{ij})=\frac{\exp(e_{ij})}{\sum_{k\in\mathcal{N}i}\exp(e{ik})} $$ 本文实验中,函数$a$实例化如下,并得到对应的$\alpha_{ij}$式子: $$ {\rm LeakyReLU}(\bold{\vec{a}}^T[\bold{W}\vec{h_i}||\bold{W}\vec{h_j}]) $$
$$ \alpha_{ij}=\frac{\exp({\rm LeakyReLU}(\bold{\vec{a}}^T[\bold{W}\vec{h_i}||\bold{W}\vec{h_j}]))}{\sum_{k\in\mathcal{N}_i}\exp({\rm LeakyReLU}(\bold{\vec{a}}^T[\bold{W}\vec{h_i}||\bold{W}\vec{h_k}]))} $$
在得到归一化的注意力系数之后,可以通过对邻接节点特征的线性组合经过一个非线性激活函数来更新节点自身的特征作为输出: $$ \vec{h_i’}=\sigma(\sum_{j\in \mathcal{N}i}\alpha_{ij}\bold{W}\vec{h_j}) $$ 进一步,为了稳定注意力效果,采取多头注意力,将计算后的结果Concat: $$ \vec{h_i’}\Vert_{k=1}^K\sigma(\sum_{j\in\mathcal{N}i}\alpha{ij}^k\bold{W}^k\vec{h_j}) $$ 其中双竖线代表拼接。
如果我们在最后一层(预测层)使用Multi-head attention mechanism,需要把输出进行平均化,再使用非线性函数(softmax或logistic sigmoid): $$ \vec{h_i’}=\sigma(\frac{1}{K}\sum_{k=1}^K\sum_{j\in\mathcal{N}i}\alpha{ij}^k\bold{W}^k\vec{h_j}) $$
GA的优点:
- 计算效率高,跨节点对可并行计算
- 可以隐式地为同一邻域的节点分配不同的重要性,也有助于模型可解释性
- 注意机制以共享的方式应用于图中的所有边,因此它不依赖于对全局图结构或所有节点(特征)的预先访问
评估
补充解释:
- Transductive learning:训练阶段与测试阶段都基于同样的图结构
- Inductive learning:训练阶段与测试阶段需要处理的图不同。通常训练阶段只是在子图(subgraph)上进行,测试阶段需要处理未知的顶点(unseen nodes)
实验结果: