【论文笔记】Neural Message Passing for Quantum Chemistry

Gilmer J, Schoenholz S S, Riley P F, et al. Neural message passing for quantum chemistry[C]//International conference on machine learning. PMLR, 2017: 1263-1272.

分子的监督学习在化学、药物发现和材料科学方面具有不可思议的潜力。幸运的是，文献中已经描述了几个有前途的和密切相关的神经网络模型，这些模型不受分子对称性的影响。这些模型学习消息传递算法和聚合过程来计算整个输入图的函数。在这一点上，下一步是找到这种通用方法的一个特别有效的变体，并将其应用于化学预测基准，直到我们解决它们或达到该方法的极限。在本文中，我们将现有模型重新制定为一个我们称为消息传递神经网络(MPNNs)的单一公共框架，并在该框架内探索其他新的变体。

使用mpnn，我们在一个重要的分子性质预测基准上展示了最先进的结果;这些结果足够强大，我们相信未来的工作应该集中在更大分子或更准确的地面真值标签的数据集上。

1 介绍

对分子结构的图监督学习已经提出了许多图神经网络模型，本文提出了MPNN框架，将这些模型都纳入这个框架当中，并探索新的变体。

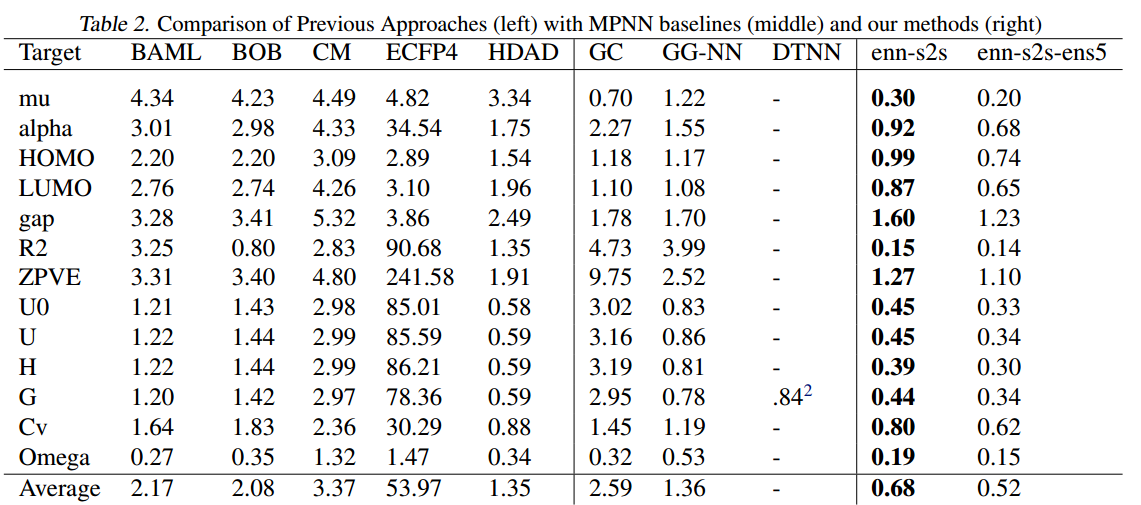
• 提出了一种MPNN，在分子预测的13个目标上实现了最先进的结果，并在其中的11个目标上达到了化学精度
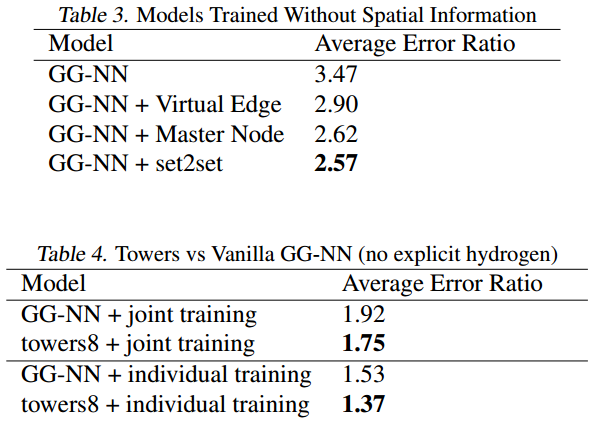
• 提出了几种不同的MPNN，在单独操作分子拓扑（没有空间信息作为输入）的情况下，在13个目标中的5个目标上达到了化学精度
• 提出了一种通用方法来训练具有更大节点表示的MPNN，而不会相应增加计算时间和内存，与以前高维节点表示的MPNN相比，节省了大量时间

2 MPNN

MPNN在无向图$G$上操作，节点特征为$x_v$，边缘特征为$e_{vw}$，可以向有向图推广。前向传播分为两个阶段：消息传递阶段和读出阶段。消息传递阶段运行$T$步，由消息函数$M_t$和定点更新函数$U_t$定义。图中每个节点的隐藏状态$h_v^t$由消息$m_v^{t+1}$更新： $$ \boldsymbol{m}_i^{k+1}=\sum _{v_j\in N(v_i)}M^{(k)}(\boldsymbol{h}_i^{(k)},\boldsymbol{h}j^{(k)},\boldsymbol{e}{ij}) $$

$$\boldsymbol{h}_i^{(k+1)}=U_i^{(k)}(\boldsymbol{h}_i^{(k)},\boldsymbol{m}_i^{(k+1)})$$

读出函数读取整个图的特征，更新特征向量： $$\hat{y}=R({h_v^T|v\in G})$$ 其中消息函数$M_t$、定点更新函数$U_t$、读出函数$R$均为可学习的可微函数。$R$作用于节点状态集合，必须不受节点状态排列的影响。

3 MPNN框架理解下的已有模型

Convolutional Networks for Learning Molecular Fingerprints, Duvenaud et al. (2015) $$M(h_v,h_w,e_{vw})=Concat(h_w,e_{vw})$$

$$U_t(h_v^t,m_v^{t+1})=Sigmoid(H_t^{deg(v)}m_v^{t+1})$$

$$R=f(\sum_{v,t}softmax(W_th_v^t))$$

Gated Graph Neural Networks (GG-NN), Li et al. (2016)

$$M(h_v,h_w,e_{vw})=A_{e_{vw}}h_w^t$$

$$U_t(h_v^t,m_v^{t+1})=GRU(h_v^t,m_v^{t+1})$$

$$R=\sum_{v,t}\sigma(i(h_v^{(T)},h_v^0))\odot(j(h_v^{(T)})$$

Interaction Networks, Battaglia et al. (2016)

$$M(h_v,h_w,e_{vw})=Concat(h_v,h_w,e_{vw})$$

$$U_t(h_v^t,m_v^{t+1})=Concat(h_v,x_v,m_v)$$

$$R=f(\sum_{v\in G}h_v^T)$$

Molecular Graph Convolutions, Kearnes et al. (2016)

$$M(h_v,h_w,e_{vw})=e_{vw}^t$$

$$U_t(h_v^t,m_v^{t+1})=\alpha(W_1(\alpha(W_0h_v^t), m_v^{t+1})$$

$$e_{vw}^{t+1}=U_t’(e_{vw}^t,h_v^t,h_w^t)=\alpha(W_4(\alpha(W_2,e_{vw}^t),\alpha(W_3(h_v^t,h_w^t))))$$

其中$\alpha$表示ReLU函数，(…,…)表示Concat连接。

Deep Tensor Neural Networks, Schutt et al. (2017)

$$M_t=tanh(W^{fc}((W^{cf}h_w^t+b_1)\odot(Q^{df}e_{vw}+b_2)))$$

$$U_t(h_v^t,m_v^{t+1})=h_v^t+m_v^{t+1}$$

$$R=\sum_v NN(h_v^T)$$

通过上述模型总结，可以寻找MPNN中的关键想法。

4 QM9数据集

数据集中的分子包括氢（H）、碳（C）、氧（O）和氮（N） ，和氟（F）原子，并且含有最多9个重（非氢）原子。总的来说，这导致了大约134k个类似药物的有机分子，这些分子跨越了广泛的化学范围。

5 MPNN变体

消息函数：

• 将分子图视为有向图，因此m向量容量变成双倍；

• 以GG-NN为基线作变体调整；

• 增加虚拟边，允许长距离传递信息

• 增加虚拟主节点，保存全局信息

读出函数：尝试了GG-NN的读出函数和set2set

输入表示：

• 化学图
• 距离箱
• 原始距离特征