【论文笔记】Relational inductive biases, deep learning, and graph networks
Battaglia P W, Hamrick J B, Bapst V, et al. Relational inductive biases, deep learning, and graph networks[J]. arXiv preprint arXiv:1806.01261, 2018.
人工智能(AI)最近经历了一次复兴,在视觉、语言、控制和决策等关键领域取得了重大进展。这在一定程度上是由于廉价的数据和廉价的计算资源,它们符合深度学习的天然优势。然而,人类智能的许多定义特征是在不同的压力下发展起来的,目前的方法仍然遥不可及。特别是,超越个人经验的概括——这是人类从婴儿期开始智能的标志——对现代人工智能来说仍然是一个巨大的挑战。
以下是部分意见书,部分回顾,部分统一。我们认为,组合泛化必须是人工智能实现类人能力的首要任务,而结构化表示和计算是实现这一目标的关键。就像生物学将先天和后天合作使用一样,我们拒绝在“手工工程”和“端到端”学习之间做出错误的选择,相反,我们提倡一种受益于两者优势互补的方法。我们探讨了如何在深度学习架构中使用关系归纳偏差来促进对实体、关系和构成它们的规则的学习。我们提出了一个具有强关系归纳偏差的AI工具包的新构建块-图网络-它概括和扩展了在图上操作的神经网络的各种方法,并为操作结构化知识和产生结构化行为提供了一个直接的接口。我们讨论了图网络如何支持关系推理和组合泛化,为更复杂、可解释和灵活的推理模式奠定基础。作为本文的补充,我们还发布了一个用于构建图网络的开源软件库,并演示了如何在实践中使用它们。
1 Intro
人类的智慧在于能够“无限地利用有限的手段”,从已知的构建块构建新的推断、预测和行为=>组合泛化能力
人类组合泛化的能力主要取决于我们表示结构和推理关系的认知机制。我们将复杂系统表示为实体及其相互作用的组合;我们使用层次结构来抽象出细粒度的差异,并捕获表征和行为之间更普遍的共性;我们通过组合熟悉的技能和惯例来解决新问题;我们通过对齐两个领域之间的关系结构,并根据对另一个领域的相应知识对其中一个领域进行推断,从而得出类比。
世界是组成的,或者至少,我们用组成的术语来理解它。在学习时,我们要么将新知识融入现有的结构化表征中,要么调整结构本身以更好地适应(并利用)新知识和旧知识。
人工智能如何获得组合泛化的能力?
- 结构化方法
- 端到端
近年来,深度学习和结构化方法的交叉领域出现了一类模型,他们关注于对显示的结构化数据进行推理的方法。这些方法的共同之处在于能够在离散的实体和他们之间的关系上进行计算,它们与经典方法的不同之处在于如何学习实体和关系的表示和结构以及相应的计算。值得注意的是,这些方法都带有强烈的关系归纳偏置,以特定的架构假设的形式来引导这些方法去学习实体和关系,这被认为是类人智能的一个重要组成部分。
2 关系归纳偏置
关系推理
我们将结构定义为组合一组已知构建块的产物。“结构化表示”捕获这种组合(即元素的排列),“结构化计算”将元素及其组合作为一个整体进行操作。因此,关系推理涉及操纵实体和关系的结构化表示,并使用规则来组合它们。我们使用这些术语来捕捉认知科学、理论计算机科学和人工智能的概念,如下所示:
-
实体是具有属性的元素,例如具有大小和质量的物理对象。
-
关系是实体之间的属性。两个对象之间的关系可能包括SAME SIZE AS, HEAVIER THAN, AND DISTANCE FROM。关系也可以有属性。大于X倍的关系接受一个属性X,该属性决定了关系的相对权重阈值是真还是假。两国关系也可能对全局上下文很敏感。对于一块石头和一根羽毛来说,下降速度的关系取决于是在空气中还是在真空中。这里我们关注实体之间的成对关系。
-
规则是一个函数(像一个非二进制逻辑谓词),映射实体和关系到其他实体和关系,如规模比较,如是实体X大吗?实体X是否比实体Y重?这里我们考虑接受一个或两个参数(一元和二元)并返回一元属性值的规则。
比较经典的例子是图模型,可以通过随机变量明确随机条件独立性来表示复杂的联合分布,如隐马尔可夫模型等;或者明确表示变量之间的稀疏依赖关系,从而提供各种有效的推理和推理算法,如消息传递等。
归纳偏置
归纳偏置允许学习算法优先考虑一种解决方案(或解释)而不是另一种解决方案,独立于观察到的数据。在贝叶斯模型中,归纳偏置通常通过先验分布的选择和参数化来表示。在其他情况下,归纳偏置可能是为了避免过拟合而添加的正则化项,或者它可能被编码在算法本身的架构中。归纳偏置通常以灵活性换取改进的样本复杂性,并且可以从偏置-方差权衡的角度来理解。理想情况下,归纳偏置既可以在不显著降低性能的情况下改善对解决方案的搜索,也可以帮助找到以理想方式推广的解决方案;然而,不匹配的归纳偏置也可能通过引入太强的约束而导致次优性能。
归纳偏置可以表达关于数据生成过程或解空间的假设。例如,在对数据拟合一维函数时,线性最小二乘法遵循近似函数为线性模型的约束,并且在二次惩罚下近似误差应最小。这反映了一种假设,即数据生成过程可以简单地解释为被加性高斯噪声破坏的直线过程。类似地,L2正则化优先考虑参数值较小的解,并且可以为病态问题导出唯一解和全局结构。这可以解释为一个关于学习过程的假设:当解决方案之间的模糊性较少时,寻找好的解决方案更容易。注意,这些假设不必是明确的——它们反映了对模型或算法如何与世界交互的解释。
通俗地说,归纳偏置让算法优先某种解决方案,这种偏好是独立于观测的数据的。它一般是对样本的产生过程,或者最终解的空间的一些假设。
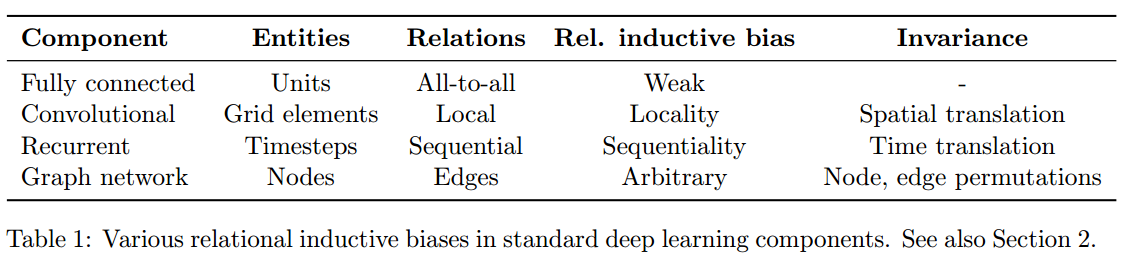
2.1 标准深度学习构建块中的关系归纳偏置
全连接层:隐式关系归纳偏置非常弱:所有输入单元可以相互作用以确定任何输出单元的值
卷积层:局部性和平移不变性
循环层:时间不变性
集合和图:集合具有排序不变性,图是一种支持任意关系结构的表示形式
3 图网络
总结大量前人的图神经网络工作,提出 GN 框架,用于图结构表示的关系推理。GN模块包括三个更新函数和三个聚合函数:
$$
\bold{e}k’=\phi^e(\bold{e}k,\bold{v}{rk},\bold{v}{sk},\bold{u}) \quad \bold{\overline{e}}_i’=\rho^{e\rightarrow v}(E_i’)\
\bold{v}_i’=\phi^v(\bold{\overline{e}}_i’,\bold{v}_i,\bold{u}) \quad \bold{\overline{e}}’=\rho^{e\rightarrow u}(E’) \
\bold{u}_i’=\phi^v(\bold{\overline{e}}’,\bold{\overline{v}},\bold{u}) \quad \bold{\overline{v}}’=\rho^{v\rightarrow u}(V’)
$$

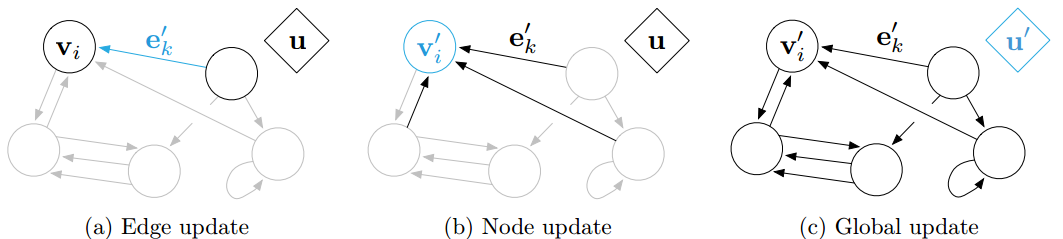
图网络的归纳偏置
- 图可以表达实体之间的任意关系,这意味着GN的输入决定了表示如何相互作用和隔离
- 图将实体及其关系表示为集合,这些集合对置换是不变的,这意味着gn对于这些元素的顺序是不变的
- GN的每边和每节点函数分别在所有边和节点上重用,这意味着GN自动支持一种形式的组合泛化
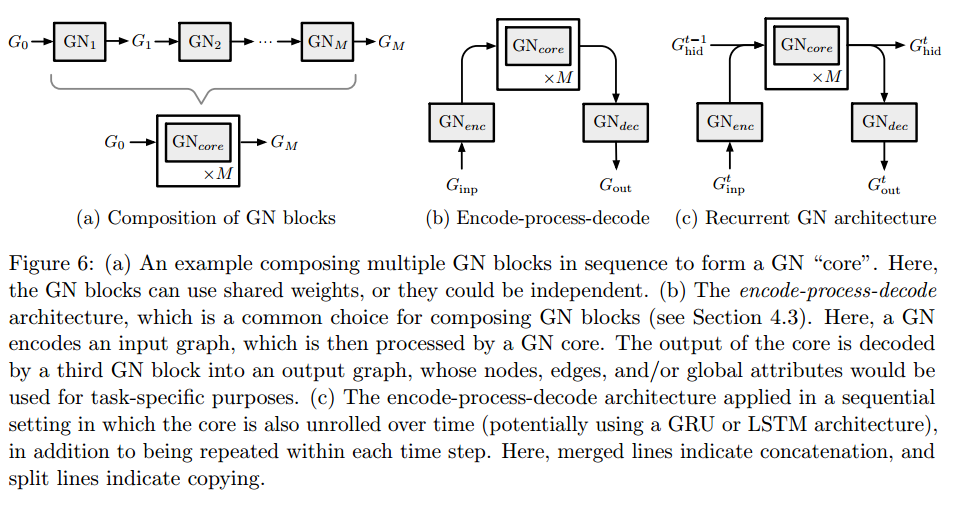
4 图网络的设计原则
- 灵活性:属性值的表征灵活性与图结构本身的灵活性
- 可配置的内部块结构
- 可组合的多块结构