【论文笔记】Reducing the dimensionality of data with neural networks

摘要

通过训练具有小中心层的多层神经网络重构高维输入向量，可以将高维数据转换为低维代码。梯度下降可以用于微调这种“自动编码器”网络中的权重，但只有当初始权重接近一个好的解决方案时，这种方法才有效。我们描述了一种有效的初始化权重的方法，该方法允许深度自编码器网络学习低维代码，这比主成分分析作为降低数据维数的工具要好得多。

Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. science, 2006, 313(5786): 504-507.

内容

我们设计了一个非线性下PCA生成器（古代的神经网络），可以使用合适、多层编码网络将高维数据转为低维编码，同时使用一个相似的解码网络来从编码数据中恢复出来。

随机初始化两个网络的权重，通过最小化原始数据和重建数据的差异来同时训练两个网络。通过链式法则来反向传播导数误差得到所需要的梯度，即通过解码网络到编码网络。整个系统被称为“自编码”。

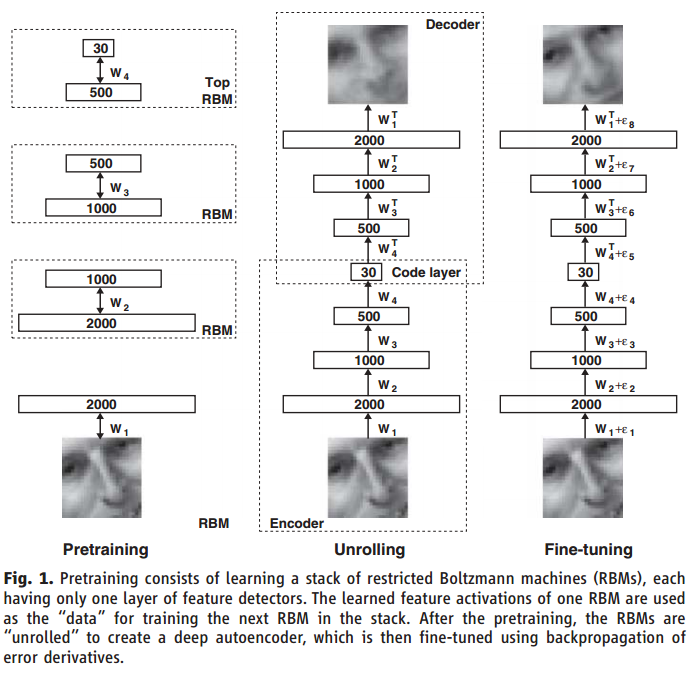
古代的BP算法具有局限性（梯度消失，没有优化器），导致初始化的结果对网络训练的结果影响很大：

• 如果随机初始化的值过大，通常会找到较差的局部极小值。个人想法这是因为较大的权值会本身就很接近某些极值或鞍点，会导致BP算法可以“操作”的空间减小了。
• 如果随机初始化的值过小，会导致前几层的梯度过小而难以训练。

我们为二进制数据引入了这种预训练过程，并将其推广到实值数据，表明它适用于各种数据集： $$ E(\bold{v},\bold{h})=-\sum_{i\in pixels}b_iv_i-\sum_{j\in features}b_jh_j-\sum_{i,j}v_ih_jw_{ij} $$ 其中$v_i$和$h_j$表示二进制像素i和特征j的状态，$b_i$和$b_j$表示其偏差，$w_{ij}$表示像素和特征之间的权重。图像的训练可以通过调整权重和偏差来降低图像的能量函数，提高能量的相似性，使“虚构的”图像更加符合真实的数据。

权重的改变：

$\Delta w_{ij}=\epsilon(<v_ih_j>{data}-<v_ih_j>{recon})$

其中$\epsilon$是学习率，被减数是像素i和特征检测器j的分数，后者是相应虚构的分数。

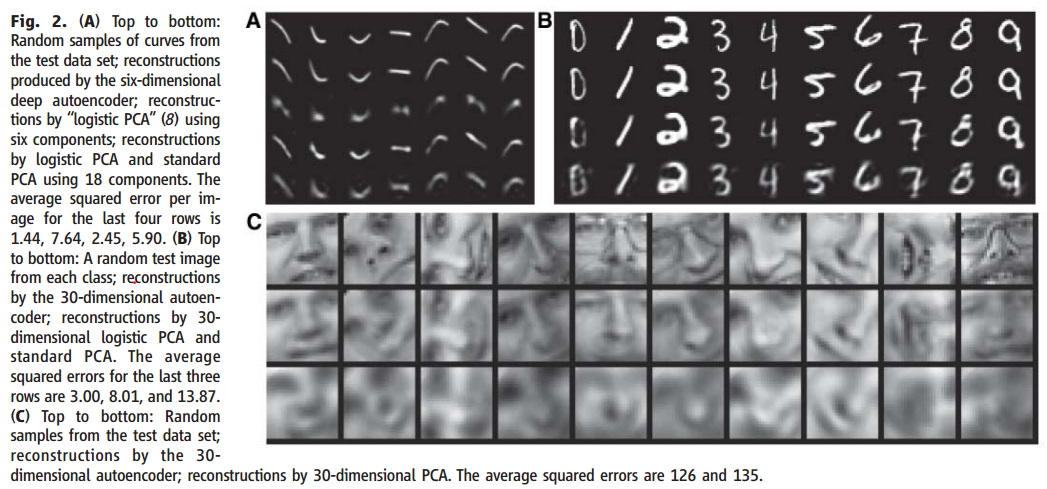
为了验证我们的预训练算法可以有效的微调我们的网络，我们使用了一个合成的曲线图数据集，改曲线图是在二维上随机选择3个自由点。对于这个数据集，真实内在的维度是已知的，像素强度和以及形成它们的非线性的6个数是相关的。像素强度在0和1之间是非高斯的，所以在自编码中我们使用逻辑输出单元，通过微调来最小化交叉熵： $$ -\sum_ip_i\log \hat{p_i}-\sum_i(1-p_i)\log(1-\hat{p_i}) $$

结论

自20世纪80年代以来，很明显，通过深度自编码器的反向传播对于非线性降维非常有效，前提是计算机足够快，数据集足够大，初始权重足够接近一个好的解决方案。现在这三个条件都满足了。与非参数方法(15,16)不同，自编码器在数据和代码空间之间给出两个方向的映射，并且它们可以应用于非常大的数据集，因为预训练和微调都随着训练案例的数量在时间和空间上呈线性增长。